这题要分成两个问题

• 可以删出来哪些字符串。
• 哪一种字符串最小。

每次删除的字符串一定从某个点开始是连续的一段。并且如果我们能删除$s[l . . . r]$，那么就可以删除$s[l..r-1]$

先来看问题1

设 $dp[c][l][r]$ 表示之前有个c的情况下，是否能删

$dp[c][l][r]=dp[c][l][m] \&\& dp[c][m+1][r]$

$O\left(n^{3} \cdot k\right)$

可以优化一下

设 $dp[c][l]=r$

$dp[c][l]=max(dp[c][l],dp[c][r])$ $(r\leq dp[c][l] \& A[c][s[r]])$

$O\left(n^{2} \cdot k\right)$

当然dp是过不去的，得用其他的方法。

用一个栈，倒序枚举，如果$i$号点 $A[s[i]][s[stack.top()]]=1$ ,那么$stack.pop()$.

否则$dp[i]=stack.top()-1$

让我们来证明这个算法。假设对于某些$dp[i]$ 是错的。考虑这些$i$中最右边的一个。我们决定该段在$y$处结束（$y=st.top() - 1$），$A[s[i]][s[y + 1]] = 0$，但实际上该段应该在$r$处结束（$y < r$）。考虑一下把删除关系建出来的树。$s[y+1]$不能是$s[i]$的直系子女。让我们从$s[y+1]$往上走，直到到达$s[i]$的孩子，让它成为$s[x]$。根据假设，对于$s[x]$，我们可以找到$y$, $y$ 一定会被$s[x]$删掉。所以当我们考虑$s[i]$时，$y$ 不可能出现在栈中。矛盾。

考虑问题2。

$ans[i]$ 表示 $s[i..n]$ 中最小的字典序字符串。那么

$ans[i]=min(ans[i],s[i]+ans[j])$

$O\left(n^{3} \right)$

如果记next而不是字符串。

$ans[i]=s[i]+s[\operatorname{next}[i]]+s[\operatorname{next}[\operatorname{next}[i]]+\ldots$

利用hash+倍增跳比较字符串，可以优化到$O\left(n^{2} logn \right)$

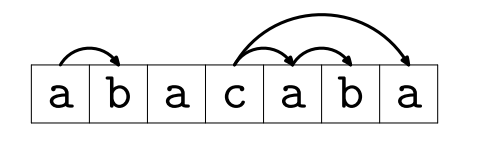
如果我们建树去做。

$$\huge ans_i=s_i+\min^{dp'[s[i]][i+1]}_{j=i+1} ans_j $$

单次询问$O(\log ^2 (n))$ ，总时间复杂度$O(n log^2(n))$

实现提示：倒序枚举，用倍增记录区间最小字符串$ans[j]$ ，每次求出$ans[i]$ ，更新倍增数组。用hash和倍增判字典序大小。

最后做法

让我们结合第一和第二部分的算法。当我们考虑$s[i]$,并从栈中删除$st.top()$时，使$ans[i] = \min(ans[i], s[i] + ans[st.top()])$。这样的算法将进行$O(n)$次比较，比较需要$O(log(n))$。总时限$O (nlog(n))$